<통계학> 분산분석(ANOVA) - 2 (One way ANOVA with Python)

 

https://jinhyunbae.tistory.com/133

<통계학> 분산분석(ANOVA) -1 (One-way-ANOVA)

 

일원배치 분산분석을 python scipy 라이브러리로 구현해보자

---

데이터 불러오기

우선 사용할 라이브러리를 import하고 데이터를 불러온다.

데이터는 가장 흔한 범주별 데이터를 담고 있는 붓꽃(iris)데이터를 이용하였다. 

iris = pd.read_csv('../data/iris.csv')
display(iris.head(10))

 

일반적으로는 머신러닝 분류에 많이 사용되는 데이터인데 일원배치 분산분석을 위해 target 데이터에 있는

값을 독립변수로 사용하고자한다.  

 

iris의 target 데이터는 setosa, versicolor, virginica의 세 품종으로 이루어져있는 것을 알 수 있고 

iris['target'].unique()

array(['Iris-setosa', 'Iris-versicolor', 'Iris-virginica'], dtype=object)

 

각각의 품종에 따라 50개의 데이터가 있는 것을 확인할 수 있다. 

iris.target.value_counts().to_frame()

target_list = iris['target'].unique()

setosa = iris[iris['target']==target_list[0]]['sepal width']
versicolor = iris[iris['target']==target_list[1]]['sepal width']
virginica = iris[iris['target']==target_list[2]]['sepal width']

 

target의 품종을 기준으로 sepal width 데이터를 3개로 나누었다. 

아래는 품종별 sepal width의 시각화 결과이다. 

sns.scatterplot(x='target', y='sepal width', 
                hue='target', style='target', 
                s=100, data=iris)
plt.show()

 

---

가설 설정

• 귀무가설 : 집단 간에 sepal width의 평균차이가 존재하지 않을 것이다.
• 대립가설 : 적어도 한 집단에 대해서는 sepal width의 평균차이가 존재할 것이다.

---

정규성 검정

집단 별로 데이터 수가 50개이기 때문에 Shapiro-Wilk 검정을 통해 정규성을 검정한다. 

print(shapiro(setosa))
print(shapiro(versicolor))
print(shapiro(virginica))

# 세 집단이 정규성 가정을 만족함
# 하나라도 만족하지 않으면 kruskal검정을 고려해야함

ShapiroResult(statistic=0.968691885471344, pvalue=0.20465604960918427)
ShapiroResult(statistic=0.9741330742835999, pvalue=0.33798879384994507)
ShapiroResult(statistic=0.9673910140991211, pvalue=0.1809043288230896)

 

세 집단 모두 p-value값이 유의수준 0.05수준보다 크기 때문에 정규성을 만족한다는 귀무가설을 기각하지 못한다. 

즉 세 집단은 정규성 가정을 만족한다.

---

등분산 검정

stats.levene(setosa, versicolor, virginica)

# 세 집단이 등분산 가정을 만족함

LeveneResult(statistic=0.6475222363405327, pvalue=0.5248269975064537)

 

 p-value값이 유의수준 0.05수준보다 크기 때문에 등분산이라는 귀무가설을 기각하지 못한다. 

즉 세 집단은 등분산성 가정을 만족한다.

---

 

One-way ANOVA

stats.f_oneway(setosa, versicolor, virginica)

F_onewayResult(statistic=47.36446140299382, pvalue=1.3279165184572242e-16)

 

p-value가 유의수준인 0.05보다 작기 때문에 적어도 한 집단에 대해서는 sepal width의 평균 차이가 있다고 할 수 있다.

---

사후 검정(Tukey)

from statsmodels.stats.multicomp import pairwise_tukeyhsd
from statsmodels.stats.multicomp import MultiComparison

mc = MultiComparison(data=iris['sepal width'], groups=iris['target'])

tukey_hsd = mc.tukeyhsd(alpha=0.05)
fig = tukey_hsd.plot_simultaneous()

tukey_hsd.summary()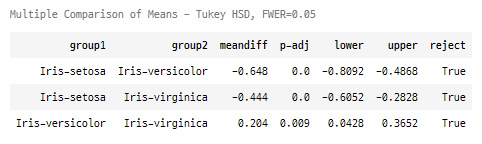

 

사후분석에서는 귀무가설을 집단들 사이의 평균은 같다로 두고 대립가설을 집단 평균은 같지 않다라고 둔다

그리고 모든 집단 수준에 대해서 두 집단씩 짝을 지어서 각각 다중비교를 수 행한다. 

 

결과를 보면 세 가지 비교에 대해서 모두 수정된 p-value값이 0.05보다 작기 때문에 유의수준 0.05수준에서 모두 귀무가설을 기각한다. 즉 모든 종에 대해 꽃받침 폭의 평균 값은 통계적으로 유의한 차이가 있다.

 

meandiff값(오른쪽 집단 - 왼쪽집단)을 보면 setosa - versicolor와, setosa - virginica 값은 음수인 것을 볼 수 있는데

이는 setosa보다  versicolor, virginica 의 꽃받침의 폭이 통계적으로 유의하게 큰 값을 가진다고 해석할 수 있다. 

---

 비모수 검정

모수 통계에 필요한 가정이 만족하지 않을 때 비모수 검정을 대신 수행할 수 있다. 

Kruskal-Wallis 검정

정규성 가정이 만족하지 않았을 때 사용

stats.kruskal(setosa, versicolor, virginica)

KruskalResult(statistic=62.49463010053111, pvalue=2.6882119006774528e-14)

 

Welch ANOVA 검정

등분산 가정이 만족하지 않았을 때 사용

import pingouin as pg

pg.welch_anova(data=iris, dv='sepal width', between='target')