<TIL> 2024-02-28

• 오늘 진행한 일 
  • SQL 코딩 테스트
  • 개인 프로젝트 (통계 분석)

---

하루 루틴인 SQL 코딩테스트 3문제를 클리어한 뒤 

개인 프로젝트 데이터에 대한 전처리 및 통계분석을 실시했다. 

 

우선 어제 EDA를 해본 결과 이상치가 데이터에 꽤 있는 것을 확인할 수 있었는데 

Z-score를 기준으로 3을 넘어가는 데이터가 425개 있는 것을 확인하였다. 

 

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

cookie_cats = pd.read_csv('./data/cookie_cats.csv')
cookie_cats

m = cookie_cats['sum_gamerounds'].mean()
s = cookie_cats['sum_gamerounds'].std()

ser_outlier_bool = ((cookie_cats['sum_gamerounds']-m)/s).abs() > 3
z_score_outliers = cookie_cats[ser_outlier_bool].sort_values('sum_gamerounds', ascending=False)
z_score_outliers

 

 

print(cookie_cats['sum_gamerounds'].mean())
print(z_score_outliers['sum_gamerounds'].mean())

51.8724567297564
1035.1858823529412

 

전체 데이터와 이상치 데이터의 평균을 비교한 결과 엄청난 차이가 있었으며

display(cookie_cats['retention_1'].value_counts(normalize=True).sort_index(ascending=False))
display(cookie_cats['retention_7'].value_counts(normalize=True).sort_index(ascending=False))
print('----------------------------------')
display(z_score_outliers['retention_1'].value_counts(normalize=True).sort_index(ascending=False))
display(z_score_outliers['retention_7'].value_counts(normalize=True).sort_index(ascending=False))

True     0.44521
False    0.55479
Name: retention_1, dtype: float64

True     0.186065
False    0.813935
Name: retention_7, dtype: float64
----------------------------------
True     0.962353
False    0.037647
Name: retention_1, dtype: float64

True     0.967059
False    0.032941
Name: retention_7, dtype: float64

 

리텐션 여부에 대한 분포도 아주 큰 차이가 있는 것을 확인하였다. 

따라서 이상치 데이터를 삭제하고 통계분석을 진행하였다. 

---

 

A/B test 결과 집단 간 게임 플레이 라운드 수의 평균 차이가 있는 지를 검증하기 위해서 

T검정을 실시하였고, 리텐션 여부에 대한 분포가 A/B 실험 처치와 독립적인지를 검증하기 위해서

카이 제곱 검정을 실시하였다. 

 

 

우선 t검정을 위해서 콜모그로프 스미노프 검정을 이용해  정규성 검정을 하였다. 

stats.ks_2samp(rm_gate_30['sum_gamerounds'], rm_gate_40['sum_gamerounds'])

KstestResult(statistic=0.010592804858190252, pvalue=0.01291146695632287)

 

유의수준 0.05 보다 p-value가 낮기 때문에 귀무가설을 기각하였고 따라서 해당 데이터는

정규성을 만족하지 않는다는 것을 확인하였다. 

 

이 경우 취할 수 있는 방법은 2가지가 있었다. 

첫 번째는 비모수 검정이고,

두 번째는 충분히 데이터가 많다는 사실을 사실을 근거로 모수 검정인 t검정을 그대로 사용하는 방법이었다.

다만 분포가 상당히 편포되어 있으므로 이를 해소하기 위해서는 로그 스케일링을 적용하였다. 

 

첫 번째인 독립 표본 t검정에 대한 비모수 검정인 만 휘트니 U검정의 결과이다. 

stats.mannwhitneyu(rm_gate_30['sum_gamerounds'], rm_gate_40['sum_gamerounds'], alternative='two-sided')

MannwhitneyuResult(statistic=1015257071.5, pvalue=0.03607620622433807)

 

비모수검정 결과 유의수준 0.05보다 p-value값이 작아서 귀무가설을 기각하였다.
따라서 집단 간의 통계적으로 유의한 차이가 있다고 할 수 있다.

---

두 번째 방법인 t검정 시행을 위해서는 등분산 검정을 할 필요가 있었다.

 

sns.histplot(np.log1p(rm_gate_30['sum_gamerounds']), label='rm_gate_30', color='blue', alpha=0.3, kde=True)
sns.histplot(np.log1p(rm_gate_40['sum_gamerounds']), label='rm_gate_40', color='red', alpha=0.3, kde=True)
plt.show()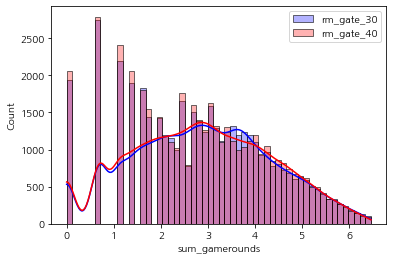

 

로그 스케일을 적용한 결과는 위 그래프와 같다. 이전에 우측 편포가 굉장히 심했던 데이터에 비해서는 편포가 

개선 된 것을 확인할 수 있다. 

 

이렇게 로그 스케일한 데이터로 등분산 검정을 시행하였다. 

stats.levene(np.log1p(rm_gate_30['sum_gamerounds']), np.log1p(rm_gate_40['sum_gamerounds']))

LeveneResult(statistic=3.176465711817767, pvalue=0.07470953545035892)

 

등분산 검정 결과 유의수준 0.5보다 p-value가 높기 때문에 귀무가설을 기각하지 않았다. 

즉 등분산성을 만족한다는 것을 확인하였고

student-t검정을 시행하였다. 

stats.ttest_ind(np.log1p(rm_gate_30['sum_gamerounds']), np.log1p(rm_gate_40['sum_gamerounds']), equal_var=True, alternative='two-sided')

Ttest_indResult(statistic=2.0306244769361155, pvalue=0.042296044430805785)

 

로그 변환 후 독립표본 t검증 결과 유의수준 0.05보다 p-value값이 작아서 귀무가설을 기각하였다.

즉 집단 간의 평균에 유의미한 차이가 있다고 할 수 있다. 

 

gate30의 플레이 라운드 수 평균이 gate40의 평균보다 통계적으로 더 크다는 결과를 얻었다. 

---

마지막으로 리텐션의 여부에 대한 카이 제곱 검정의 결과이다. 

리텐션은 인스톨 후 1일 뒤의 플레이 여부인 retention_1과 7일 뒤 플레이 여부인 retention_7이 있었고

각각 True False의 불리언 형태 데이터였기 때문에 독립성 검정을 시행하여 각각의 집단이 독립인지를 검증하였다. 

 

검증 결과는 다음과 같다. 

rm_rt_table1 = pd.crosstab(cookie_cats_rm_outlier['version'], cookie_cats_rm_outlier['retention_1'])
chi_1r, p_1r, df_1r, expect_1r = stats.chi2_contingency(rm_rt_table1)

print('통계량', chi_1r)
print('p-value', p_1r)
print('자유도', df_1r)
print('기대값', expect_1r)

통계량 3.572427509836186
p-value 0.058746373496203416
자유도 1
기대값 [[24797.13470879 19702.86529121]
 [25222.86529121 20041.13470879]]

 

retention1의 경우 유의수준 0.05보다 p-value값이 크므로 귀무가설을 기각하지 않는다. 
따라서 version과  retention_1은 독립적이라고 할 수 있다. 

rm_rt_table7 = pd.crosstab(cookie_cats_rm_outlier['version'], cookie_cats_rm_outlier['retention_7'])

chi_7r, p_7r, df_7r, expect_7r = stats.chi2_contingency(rm_rt_table7)
print('통계량', chi_7r)
print('p-value', p_7r)
print('자유도', df_7r)
print('기대값', expect_7r)

통계량 11.383737192188153
p-value 0.0007408990400188393
자유도 1
기대값 [[36384.66423065  8115.33576935]
 [37009.33576935  8254.66423065]]

 

retention7의 경우 유의수준 0.05보다 p-value값이 작기 때문에 귀무가설을 기각한다.
유의확률 0.0007로 상당히 유의한 것으로 나타났다. 

따라서 version과 retention_7은 독립적이지 않다. 
다시 말해 version에 따라 retention_7 여부가 다르다고 할 수 있다. 

---

display(rm_gate_30['retention_7'].value_counts(normalize=True).sort_index(ascending=False))
print('-------------------')
display(rm_gate_40['retention_7'].value_counts(normalize=True).sort_index(ascending=False))

True     0.186764
False    0.813236
Name: retention_7, dtype: float64
-------------------
True     0.178044
False    0.821956
Name: retention_7, dtype: float64

 

gate30과 gate40의 리텐션 여부 분포를 보면 40의 False 비율이 30보다 조금 높은 것을 확인할 수 있다. 

이를 해석하면 gate 40의 경우가 retention 지표가 더 낮다고 해석할 수 있다. 

 

유저에게 게임을 어렵게 만들어 시간 혹은 돈을 소모하게 만드는 장벽을 레벨 30에 설치했을 때와 

레벨 40에 설치했을 때를 비교한 A/B 테스트의 통계 분석 결과는 

 

기존 30레벨 구간에 설치 되었을 때에 비해 40레벨에 설치되었을 때 플레이 라운드 수도 줄어들었고 retention 또한 

낮아졌다고 할 수 있다. 따라서 기존 레벨 대인 30레벨로 유지하는 것이 좋겠다는 결론을 내리게 되었다.

---

내일은 팀프로젝트를 하느라 바쁠 예정이다. 이제 발제가 시작되니 열심히 주제를 정하고 데이터를  찾을 것 같다.

 

오늘 분석한 내용에 대해서 튜터님께 최종적으로 질문을 드린 뒤  한 번 점검해보는 시간을 가지고 

주말을 이용해서 이를 태블로 대시보드로 작성하고자 한다.