<통계학> 분산분석(ANOVA) - 4 (Two-way ANOVA with Python)

https://jinhyunbae.tistory.com/136

<통계학> 분산분석(ANOVA) - 3 (Two-way ANOVA)

 

이원배치 분산분석을 python scipy 라이브러리로 구현해보자

---

데이터 불러오기

우선 사용할 라이브러리를 import하고 데이터를 불러온다.

사용한 데이터는 R 내장데이터인 mtcars를 이용했다. 

mtcars = pd.read_csv('../data/mtcars.csv')
display(mtcars.head(10))

 

우리는 이 중에서 mpg(연비), 실린더(cyl), 변속기 종류(am) 변수를 사용할 것이다. 

연비는 연속형 변수이고, 실린더 개수와 변속기 종류는 이산형 변수이다. 

mtcars[['mpg']].describe()

mtcars.cyl.value_counts().sort_index().to_frame()

mtcars.am.value_counts().sort_index().to_frame()

---

가설 설정

주효과

• 귀무가설 1 : 실린더 개수에 따른 연비 차이는 존재하지 않는다. 
• 대립가설 1 : 실린더 개수에 따른 연비 차이는 존재한다. 

 

주효과 2

• 귀무가설 2 : 변속기 종류에 따른 연비 차이는 존재하지 않는다. 
• 대립가설 2 : 변속기 종류에 따른 연비 차이는 존재한다. 

 

교호작용 효과

• 귀무가설 3 : 연비에 대한 변속기 종류와 실린더 개수 간에는 상호작용 효과가 없다.
• 대립가설 3 : 연비에 대한 변속기 종류와 실린더 개수 간에는 상호작용 효과가 있다.

---

통계적 가정 검정

우선 정규성과 등분산성을 만족한다는 가정하에 분석을 진행하겠다. 

정규성과 등분산성 가정에 대한 코드는 일원배치 분산분석 링크에서 확인할 수 있다. 

 

https://jinhyunbae.tistory.com/134

<통계학> 분산분석(ANOVA) - 2 (One way ANOVA with Python)

 

이원배치 분산분석의 비모수 검정의 경우에는 일원배치 때와 마찬가지로 

Mann-Witney를 pairwise하게 시행한 뒤 Bonferroni Correction 하는 방법으로 진행해야하지 싶다. 

---

Two-way ANOVA

from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm

formula = 'mpg ~ C(cyl) + C(am) + C(cyl):C(am)'
model = ols(formula, mtcars).fit()

anova_table = anova_lm(model, typ=2)
anova_table

 

 

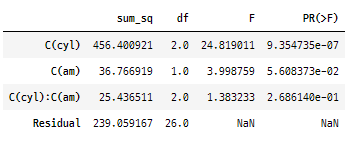
cyl변수의 주효과는 p-value가 0.5보다 작기 때문에 귀무가설을 기각함
am변수의 주효과는 p-value가 0.5보다 크기 때문에 귀무가설 기각하지 않음
cyl변수와 am변수의 상호작용효과는 p-value가 0.5보다 크기 때문에 귀무가설을 기각하지 않음

 

결과 cyl에 대한 주효과만 확인하였다. 

---

교호 작용 그래프 확인

from statsmodels.graphics.factorplots import interaction_plot

cyl = mtcars['cyl']
am = mtcars['am']
mpg = mtcars['mpg']

fig, ax = plt.subplots(figsize=(6,6))

fig = interaction_plot(cyl, am, mpg, 
                       colors=['red', 'blue'], markers=['D', '^'], 
                       ms=10, ax=ax)

# intercation_plot 매개변수는 x1, x2, y 순으로 작성해야함

 

교호작용이 나타나지 않았지만 statsmodels에서 위처럼

interaction_plot(상호작용 그래프)를 그릴 수 있다.